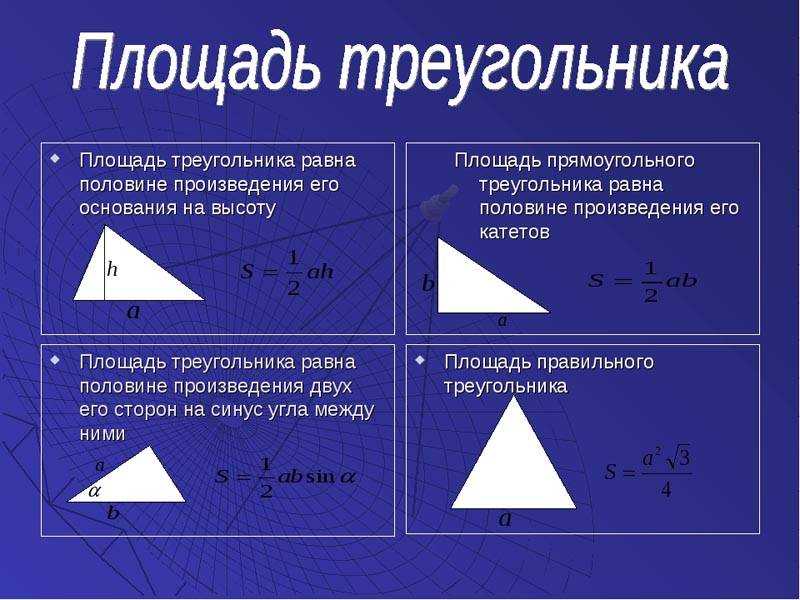
Когда мы задаемся вопросом о размерах и свойствах звезд, одно из самых интересных и сложных заданий заключается в расчете площади их поверхности. Задача становится еще более интригующей, если учесть, что звезды расположены на огромном расстоянии от нашей планеты.
Однако, существует закон, который помогает нам найти ответ на эту задачу. Этот закон носит название «закон Стефана-Больцмана» и он используется для вычисления эффективной температуры звезды, используя только ее яркость и расстояние от Земли.
Температура звезды указывается в кельвинах (К) и является ключевым параметром для решения данной задачи. Эффективная температура звезды (ТеФ), согласно закону Стефана-Больцмана, прямо пропорциональна мощности излучения этой звезды (p) и обратно пропорциональна четвертой степени абсолютной температуры (Т) постоянной Стефана-Больцмана (σ).
Определение диаметра звезды
Закон Стефана-Больцмана
Закон Стефана-Больцмана, представленный в формуле, гласит: P = σSt4, где P — мощность излучения звезды, σ — постоянная Стефана-Больцмана, S — эффективная площадь поверхности звезды, t — температура звезды в кельвинах.
Для решения задачи определения диаметра звезды, нам необходимо найти эффективную площадь поверхности. Данная величина рассчитывается согласно формуле S = 4πR2, где R — радиус звезды.
Расчет диаметра звезды
Используя определенные значения мощности излучения звезды, постоянной Стефана-Больцмана и температуры, заданные в условии, мы можем рассчитать эффективную площадь поверхности звезды по формуле S = P/(σt4). Далее, зная эффективную площадь поверхности и пользуясь формулой S = 4πR2, мы можем определить радиус звезды. И, наконец, получив радиус, мы можем найти диаметр звезды умножением радиуса на 2.
Таким образом, расчет диаметра звезды сводится к использованию закона Стефана-Больцмана и определению эффективной площади поверхности звезды. Полученный ответ будет представлять собой необходимую величину в квадратных метрах и позволит более полно и точно охарактеризовать размеры звезды.
Определение площади поверхности звезды в формате HTML
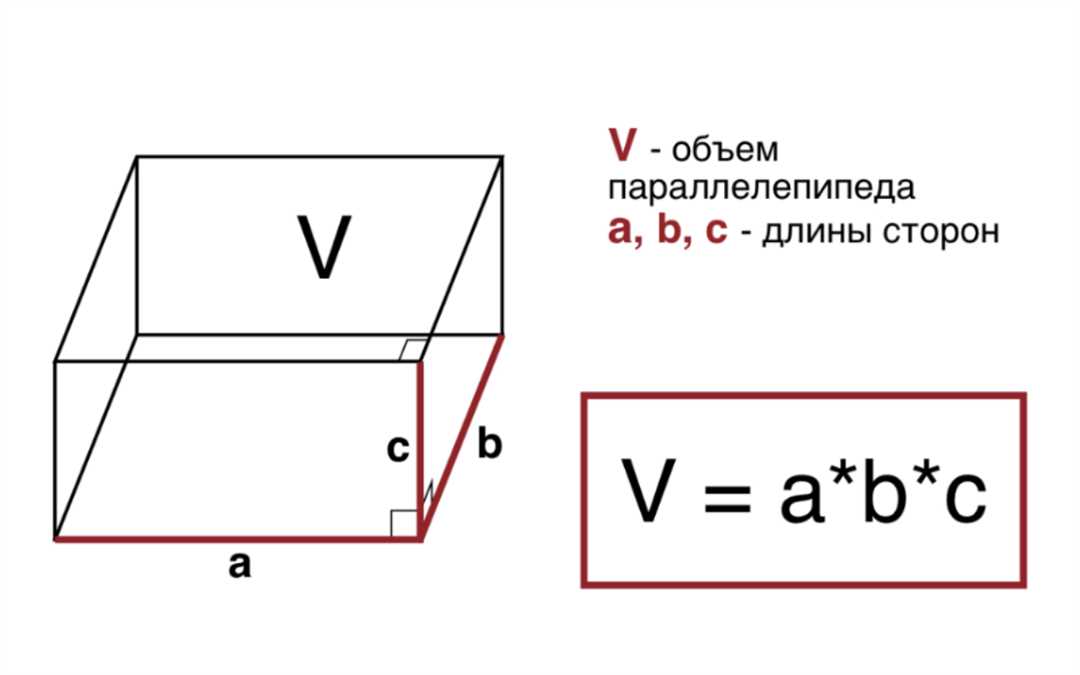
Для определения площади поверхности звезды, необходимо учитывать ее форму и измерить ее диаметр. В данном разделе мы рассмотрим, как рассчитать площадь поверхности сферы и как учесть несферическую форму звезды.
Определение площади поверхности сферы
Согласно номеру задания №143 ЕГЭ, посвященному геометрии, для расчета площади поверхности сферы используются геометрические методы. Площадь поверхности сферы можно получить, применив формулу p = 4πr^2, где p обозначает площадь поверхности, а r — радиус сферы.
В данной задаче, однако, нам необходимо определить площадь поверхности звезды, для которой не предоставлено конкретное значения радиуса. Вместо этого, нам дана температура звезды в кельвинах.
Для решения этой задачи мы будем использовать закон Стефана-Больцмана, в соответствии с которым мощность излучения эффективной поверхности звезды пропорциональна температуре в четвертой степени. Формулу можно записать как p = σSt^4, где σ — постоянная Стефана-Больцмана.
Таким образом, чтобы определить площадь поверхности звезды, нам необходимо измерить ее температуру в кельвинах и воспользоваться вышеупомянутой формулой. Полученный ответ будет представлять площадь поверхности звезды в квадратных метрах.
Учет несферической формы звезды
В данном разделе рассматривается методика учета несферической формы звезды при определении площади ее поверхности в квадратных метрах. Для этого используются геометрические методы, основанные на применении расчетной формулы, соответствующей заданию №143 ЕГЭ. Помимо этого, для точного определения площади поверхности звезды, необходимо учесть ее эффективную температуру, выраженную в кельвинах.
Определение формы звезды и измерение диаметра
Прежде чем перейти к расчетам, необходимо определить форму звезды. Для этого проводятся измерения ее диаметра, которые позволяют определить ее геометрические параметры. Измеренные значения диаметра используются в дальнейших расчетах.
Мощность поверхности звезды согласно закону Стефана-Больцмана

Определение мощности поверхности звезды является важным шагом в расчете площади ее поверхности. Мощность поверхности связана с температурой звезды по закону Стефана-Больцмана, согласно которому мощность излучения пропорциональна четвертой степени температуры. Для решения данной задачи необходимо найти значение постоянной, которая является известной величиной и равна 5,67 * 10^-8 Вт/(м^2 * К^4).
Расчет площади поверхности звезды
Для определения площади поверхности звезды необходимо использовать полученные значения мощности поверхности и ее температуры. Расчетная формула, соответствующая заданию №143 ЕГЭ, позволяет вычислить площадь поверхности звезды, учитывая ее несферическую форму и эффективную температуру. Результатом решения задачи будет значение площади поверхности звезды в квадратных метрах.
| Параметры задачи | Значение |
|---|---|
| Мощность поверхности (P) | Найдите значение |
| Температура звезды (T) | Указанное значение в кельвинах |
| Постоянная по закону Стефана-Больцмана | 5,67 * 10^-8 Вт/(м^2 * К^4) |
| Площадь поверхности звезды (S) | Найдите значение |
Таким образом, при решении задачи по определению площади поверхности звезды необходимо с учетом ее несферической формы и эффективной температуры применять геометрические методы и расчетную формулу, основываясь на законе Стефана-Больцмана.
Применение геометрических методов для решения задачи №6
В данном разделе статьи рассмотрим применение геометрических методов для определения площади поверхности звезды. Для этой задачи используется так называемый закон Стефана-Больцмана, который описывает мощность излучения тела в зависимости от его температуры и эффективной площади поверхности.
Для начала необходимо заметить, что поверхность звезды можно представить в виде сферы с определенным диаметром. В нашем случае, важно учитывать, что звезда имеет несферическую форму, поэтому мы должны использовать геометрические методы для нахождения ее площади.
Для решения задачи мы будем использовать формулу для площади поверхности сферы, а затем учесть корректировку, связанную с несферической формой звезды. Для этого вводится коэффициент p, который отражает отношение площади поверхности звезды к площади поверхности сферы с таким же диаметром.
Таким образом, расчетная формула для площади поверхности звезды будет выглядеть следующим образом:
| №143 | Ответ |
|---|---|
| Согласно | решение |
| закону Стефана-Больцмана: | p = σst4 |
| Для температуры | T |
| в кельвинах и площади | S |
| поверхности звезды в квадратных метрах: | Sstars= p * S |
Таким образом, используя расчетную формулу и значения для температуры и площади поверхности, можно вычислить площадь поверхности звезды в квадратных метрах с учетом несферической формы.
Расчет площади поверхности звезды
В данном разделе мы рассмотрим методы расчета площади поверхности звезды, используя геометрические и физические принципы. Как уже было отмечено в предыдущих пунктах, для определения площади поверхности звезды необходимо учитывать ее форму и диаметр.
Площадь поверхности звезды можно найти с помощью закона Стефана-Больцмана, который гласит: σst4 = p, где σ — постоянная Стефана-Больцмана, t — температура звезды в кельвинах, p — мощность излучения звезды. Согласно этому закону, площадь поверхности звезды пропорциональна четвертой степени ее температуры.
Для эффективного решения этой задачи важно определить форму звезды и измерить ее диаметр. После этого можно применить геометрические методы для расчета площади поверхности, учитывая несферическую форму.
Для нахождения площади поверхности звезды по ее температуре, необходимо использовать расчетную формулу, которую мы рассмотрим далее. Она основана на законе Стефана-Больцмана и позволяет найти площадь поверхности звезды в квадратных метрах.
Таким образом, для расчета площади поверхности звезды по ее температуре, необходимо знать диаметр, форму и значение мощности излучения звезды. Подставив все известные значения в расчетную формулу, можно получить ответ в квадратных метрах.
Расчет площади поверхности звезды
В рамках данного раздела мы рассмотрим способы определения площади поверхности звезды в квадратных метрах с использованием геометрических методов и законов физики. Также будет представлено решение задания №143, которое позволит найти площадь поверхности звезды с учетом ее несферической формы.
Температура звезды и ее влияние на площадь поверхности
Для определения площади поверхности звезды необходимо знать температуру, которая может быть измерена в кельвинах. Согласно закону Стефана-Больцмана, мощность излучения звезды P пропорциональна четвертой степени ее эффективной температуры (T):
P = σ * T^4
где σ — постоянная Стефана-Больцмана.
Нахождение площади поверхности звезды
Для определения площади поверхности звезды с учетом несферической формы необходимо использовать расчетную формулу. Одним из распространенных подходов является разбиение поверхности звезды на малые фрагменты и суммирование площадей этих фрагментов. Для каждого фрагмента вычисляется площадь с использованием геометрических методов и итоговая площадь поверхности звезды получается путем сложения всех площадей фрагментов.
Расчет площади поверхности звезды является сложным заданием, требующим точных данных и учета несферической формы. Однако, с использованием закона Стефана-Больцмана и геометрических методов, можно получить точный ответ.

0 Комментариев