В мире геометрии существует множество разнообразных фигур и форм, которые могут быть использованы для создания уникальных трехмерных объектов. Одной из таких удивительных фигур является призма с основанием в форме звезды. Эта особенная призма отличается своими уникальными свойствами и находит широкое применение в различных областях.
В отличие от обычной призмы, у которой основания являются прямоугольниками, у призмы с основанием в форме звезды боковые грани представляют собой многоугольники, у которых число сторон может быть различным. Это позволяет сделать призму более сложной и интересной, отличающейся от обычных форм.
Преимущество призмы с основанием в форме звезды заключается в том, что она создает более привлекательный внешний вид и является более устойчивой конструкцией. Звездообразная форма оснований призмы позволяет сборку деталей без использования лишних элементов или клея, достигая при этом прямые и равные грани.
Отличие правильной призмы от прямой призмы
Особенности правильной призмы
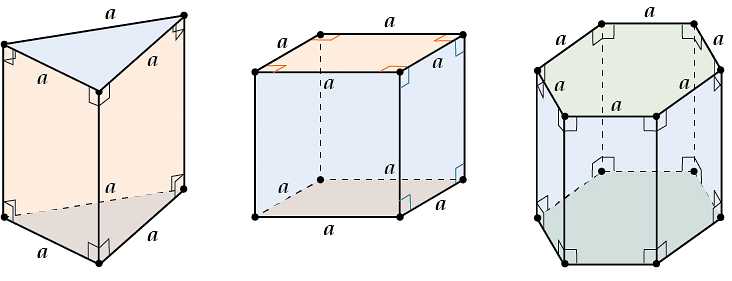
Правильная призма является особой формой призмы, в которой все боковые грани являются равными прямоугольниками. Таким образом, основания правильной призмы являются равными многоугольниками (например, правильный треугольник, правильный четырехугольник и т.д.), а боковые грани — равными прямоугольниками.
Важной особенностью правильной призмы является то, что ее оси перпендикулярны основаниям. Это означает, что линия, соединяющая центры оснований, является перпендикуляром ко всем боковым граням. Кроме того, все грани правильной призмы являются плоскими и параллельными друг другу.
Особенности прямой призмы
Прямая призма также является разновидностью призмы, у которой основания являются прямоугольниками. Отличие прямой призмы от правильной заключается в том, что ее боковые грани не являются равными прямоугольниками, а могут быть прямоугольниками любых размеров. Поэтому у прямой призмы основания и боковые грани могут иметь разные размеры и формы.
Прямая призма является популярным объектом изучения в геометрии и имеет широкое применение в различных областях, включая архитектуру, строительство, графику и дизайн. Благодаря своим особенностям, прямая призма может быть использована в качестве основы для создания многогранников и конструкций различной сложности.
Примеры применения правильной и прямой призмы
Примерами применения правильной и прямой призмы могут служить различные постройки и конструкции. Например, правильная призма может быть использована как основа для создания геометрических моделей или игрушек для детей. Также правильные призмы широко применяются в архитектуре и строительстве при создании фасадов и декоративных элементов.
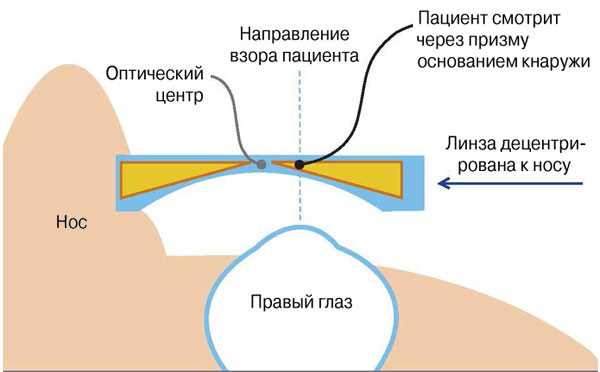
Прямая призма, благодаря своим свойствам, может быть использована в качестве основания для создания столов, полок или других предметов мебели. Также прямые призмы используются в оптике и фотографии для создания различных эффектов и фильтров.
| Правильная призма | Прямая призма |
|---|---|
| Основания — равные многоугольники | Основания — прямоугольники любых размеров |
| Боковые грани — равные прямоугольники | Боковые грани — прямоугольники разных размеров |
| Оси перпендикулярны основаниям | Оси не обязательно перпендикулярны основаниям |
| Применяется для создания геометрических моделей и конструкций | Применяется в архитектуре, строительстве, оптике и фотографии |
Основные понятия и свойства правильной призмы

Правильная призма имеет дно и верх, которые являются основаниями данной геометрической фигуры. Эти основания представляют собой многоугольники, на которые накладываются боковые прямоугольники, образуя объемное тело. В общем случае, основаниями могут быть любые многоугольники, но в случае правильной призмы, они являются равными и подобными фигурами.
Свойства правильной призмы:
- Основания правильной призмы являются полигонами с равными сторонами и равными углами.
- Все боковые грани правильной призмы представляют собой прямоугольники.
- Высота правильной призмы является перпендикуляром к основаниям и равна расстоянию между ними.
- Площадь боковой поверхности правильной призмы равна сумме всех площадей боковых граней.
- Объем правильной призмы определяется как произведение площади основания на высоту.
Готовый набор призм представляет собой набор из нескольких правильных призм разных размеров и форм, который можно использовать в различных областях. Такой набор может быть полезен для изучения геометрии, проведения экспериментов, визуализации объемов и теоретических рассчетов. Множество возможностей применения правильных призм делает их популярными инструментами в образовательных и научных целях.
Прямая призма и ее характеристики
Особенности прямой призмы
Важной особенностью прямой призмы является ее форма оснований — прямоугольники. Это дает возможность призме иметь ровные и параллельные боковые грани, что в свою очередь позволяет ей иметь правильную форму и симметрию. Правильная прямая призма является фигурой, которая имеет все грани и углы равными между собой. Такой тип прямой призмы обладает определенными свойствами, такими как правильный объем, устойчивость и легкость сборки.
Применение прямой призмы
Прямая призма находит применение в разнообразных областях, благодаря своим характеристикам. Она используется в архитектуре для создания трехмерных моделей зданий, в графике для создания пространственных изображений, в оптике для построения оптических систем, в математике для решения различных задач и упражнений, а также в промышленности для изготовления различных изделий и деталей.
Правильная призма: определение и особенности
Правильная призма является многогранником, у которого основаниями служат равные правильные многоугольники, а боковые грани — прямоугольники. Из этого определения можно выделить две ключевые особенности призмы:
- Основания: правильные многоугольники, которые могут быть круглыми, треугольными, четырехугольными и другими формами.
- Боковые грани: прямоугольники, которые соединяют основания призмы. Они обладают равными сторонами и прямыми углами.
Сборка правильной призмы из бумаги является популярным занятием, которое позволяет не только изучить ее структуру, но и развить творческие навыки. Для этого можно использовать готовый набор деталей, которые представляют собой вырезанные из бумаги основания и полоски для боковых граней. Сборка такой призмы требует аккуратности и точности, чтобы грани и углы соединения были ровными и стабильными.
Правильная призма имеет широкое применение в различных областях, начиная от геометрии и архитектуры, и заканчивая строительством и наукой. Она может быть использована в качестве моделей зданий, блоков для создания 3D-моделей, элементов для декора и даже в научных экспериментах.
Итак, правильная призма представляет собой многогранник, у которого основаниями служат равные правильные многоугольники, а боковые грани — прямоугольники. Ее можно изготовить из бумаги, используя готовые детали или создавая их самостоятельно. Этот многогранник является популярным и находит применение в различных областях, от геометрии до научных экспериментов.
Готовый набор правильных призм: популярные варианты и возможности использования
В частности, готовые наборы правильных призм из бумаги являются отличным инструментом для изучения геометрии и пространственных фигур. Такие наборы обычно включают несколько призм различных размеров и форм, которые можно легко собрать и использовать для визуализации и изучения основных свойств призм, таких как объем и боковые грани.
Боковые грани правильной призмы представляют собой параллельные прямоугольники, которые могут быть различных размеров и форм. Однако, независимо от варианта формы, все они имеют одну общую особенность — равные стороны. Благодаря этому свойству, призма обладает определенной симметрией и регулярным структурным устройством.
Использование готовых наборов призм из бумаги позволяет провести сборку и изучение свойств различных видов призм. Основаниями таких наборов могут быть как прямоугольные, так и четырехугольные формы. Правильные прямоугольные призмы являются наиболее распространенными и популярными, благодаря своей простоте и удобству использования.
Вместе с тем, наборы правильных четырехугольных призм также представляют интерес и являются небольшими практическими примерами применения правильных призм в разных областях. Такие призмы могут иметь различные размеры оснований и боковых граней, что позволяет изучать разнообразие форм и структур призм.
Таким образом, готовые наборы правильных призм из бумаги представляют собой удобный инструмент для изучения и визуализации основных свойств призм. Их разнообразие включает как прямоугольные, так и четырехугольные формы, которые позволяют проводить изучение и эксперименты с разными параметрами и характеристиками данных геометрических фигур.
Варианты формы и применение правильных призм
Правильная прямоугольная призма
Одним из самых распространенных вариантов формы призмы является прямоугольная призма. Ее основаниями являются прямоугольники, а боковые грани представляют собой параллелограммы. Такая призма отличается особой устойчивостью и прочностью, что делает ее востребованной в строительной отрасли. Прямоугольные призмы также находят широкое применение в геометрии и математике для иллюстрации различных геометрических понятий и задач.
Правильная четырехугольная призма
Другим интересным вариантом формы призмы является правильная четырехугольная призма. В этом случае основаниями служат четырехугольники, а боковые грани представляют собой прямоугольники. Этот тип призмы обладает некоторыми особенностями, которые отличают его от других видов призм. Например, угол между боковой гранью и основанием может быть различным в зависимости от формы основания: треугольного, квадратного, прямоугольного и т.д. В связи с этим правильная четырехугольная призма широко используется в конструктивных решениях и архитектуре, где требуется учет геометрических особенностей данного типа призмы.
Готовые наборы призм предлагают широкий выбор форм и размеров, что позволяет находить применение им в различных областях — от образования и научных исследований до декоративного дизайна. Благодаря уникальным свойствам правильных призм и их разнообразию, каждый может найти наиболее подходящий вариант для своих нужд.
Разнообразные формы и возможности правильных призм
Прямая призма является одной из разновидностей правильной призмы, в которой боковые грани являются прямоугольниками. Она отличается от прямой призмы формой основания и формой боковых граней. Правильная призма представляет собой многогранник с равными основаниями, у которого боковые грани представляют собой прямоугольники. Призма изготавливается из различных материалов, но в данном случае мы рассмотрим, как сделать призму из бумаги.
Сборка призмы из бумаги происходит по следующей схеме: нужно вырезать две идентичные боковые поверхности и одну верхнюю и нижнюю поверхности — основания. Боковые грани должны быть равными прямоугольниками, а основания — многоугольниками. Затем необходимо сложить боковые грани и прикрепить их к основаниям, образуя трехмерную фигуру.
Правильные призмы имеют множество применений в разных областях. Они могут использоваться в геометрии для визуализации геометрических проблем, в архитектуре для создания объемных моделей зданий, в физике для рассмотрения пространственных конструкций, а также в дизайне и искусстве для создания интересных и оригинальных объектов. Готовые наборы призм предлагают много вариантов формы призмы и позволяют использовать их в различных сферах деятельности.
Правильная четырехугольная призма — это особый вид правильной призмы, в которой основаниями являются четырехугольники. Она может быть использована для создания уникальных моделей и представлена в различных областях, от науки и техники до образования и творчества.
Боковые грани и объем прямой призмы
Боковые грани прямых призм могут быть различной формы и размера. Они могут быть прямоугольными, квадратными или других многоугольных форм. Однако, отличительной особенностью прямых призм является то, что боковые грани всегда представляют собой прямоугольники, а основания могут быть разными по форме и размеру.
Объем прямой призмы вычисляется по формуле: V = S * h, где V — объем, S — площадь основания, h — высота призмы. Зная площадь основания и высоту, мы можем определить объем прямой призмы.
Прямые призмы очень популярны в различных областях, таких как архитектура, геометрия, инженерное дело и другие. Их конструкция позволяет использовать их в качестве деталей для создания различных объектов и сооружений. Например, прямая призма может быть использована для создания каркаса здания или выступать в качестве основания некоторых архитектурных элементов.
Таким образом, боковые грани и объем прямой призмы являются важными характеристиками, определяющими ее форму и применение. Разнообразие форм боковых граней позволяет создавать различные конструкции с применением прямых призм, а знание объема позволяет определить ее вместимость и функциональные возможности.

0 Комментариев