Математика — это наука о числах, формах и пространстве. Изучение геометрии и вычисления площадей фигур являются неотъемлемой частью образования. Но что, если эти стандартные подходы и формулы уже не могут удовлетворить новые потребности учащихся?
Преодоление старых методов и поиск новых решений — вот непростая задача, с которой сталкиваются учителя и ученики сегодня. Учебный процесс переопределен, и теперь нужно искать новые подходы к обучению математике.
Один из новых подходов — использование метода урок-моделирования. Но почему именно он? Во-первых, урок-моделирования позволяет ученикам решать задачи, используя конкретные модели и математические представления. Во-вторых, данный метод развивает умение работать с геометрическими фигурами и вычислять их площади.
Например, для вычисления площади прямоугольника ученик может использовать аналитическую формулу «площадь равна произведению длины на ширину». Или же учитель может предложить менее прямолинейный подход — рассмотреть прямоугольник как совокупность точек на плоскости и вычислить площадь по количеству этих точек.
Также в рамках урока-моделирования ученики могут изучать особенности вычисления площади треугольника. Используя модели и геометрические преобразования, они могут найти решение задачи.
В итоге, полученное количественное значение площади фигуры изображено в определенных единицах измерения. Отличие нарисованной площади на карте от результатов ученого может быть заключено, например, в единичном радиусе.
Именно такие новые методы и подходы позволяют ученикам с большим интересом исследовать математику и находить решения сложных задач. Уроки, в которых содержится моделирование и аналитические формы вычисления, обеспечивают более полное и глубокое понимание площади фигур и развивают умение решать математические задачи.
Конечно, классические методы и формулы остаются важными и необходимыми в обучении, но использование новаторских подходов делает уроки более интересными и эффективными.
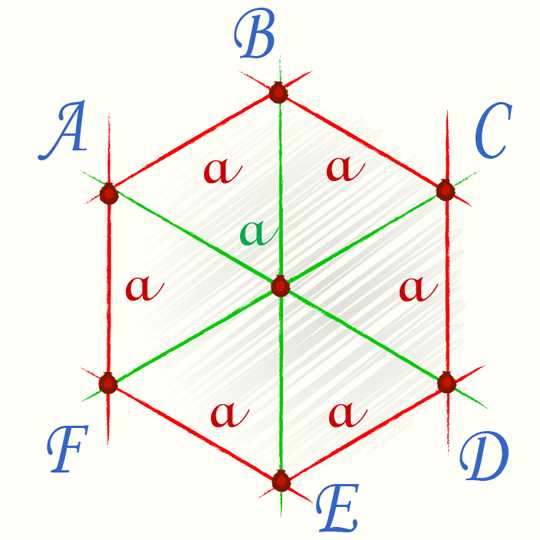
Метод измерения площади звезды с помощью геометрических форм
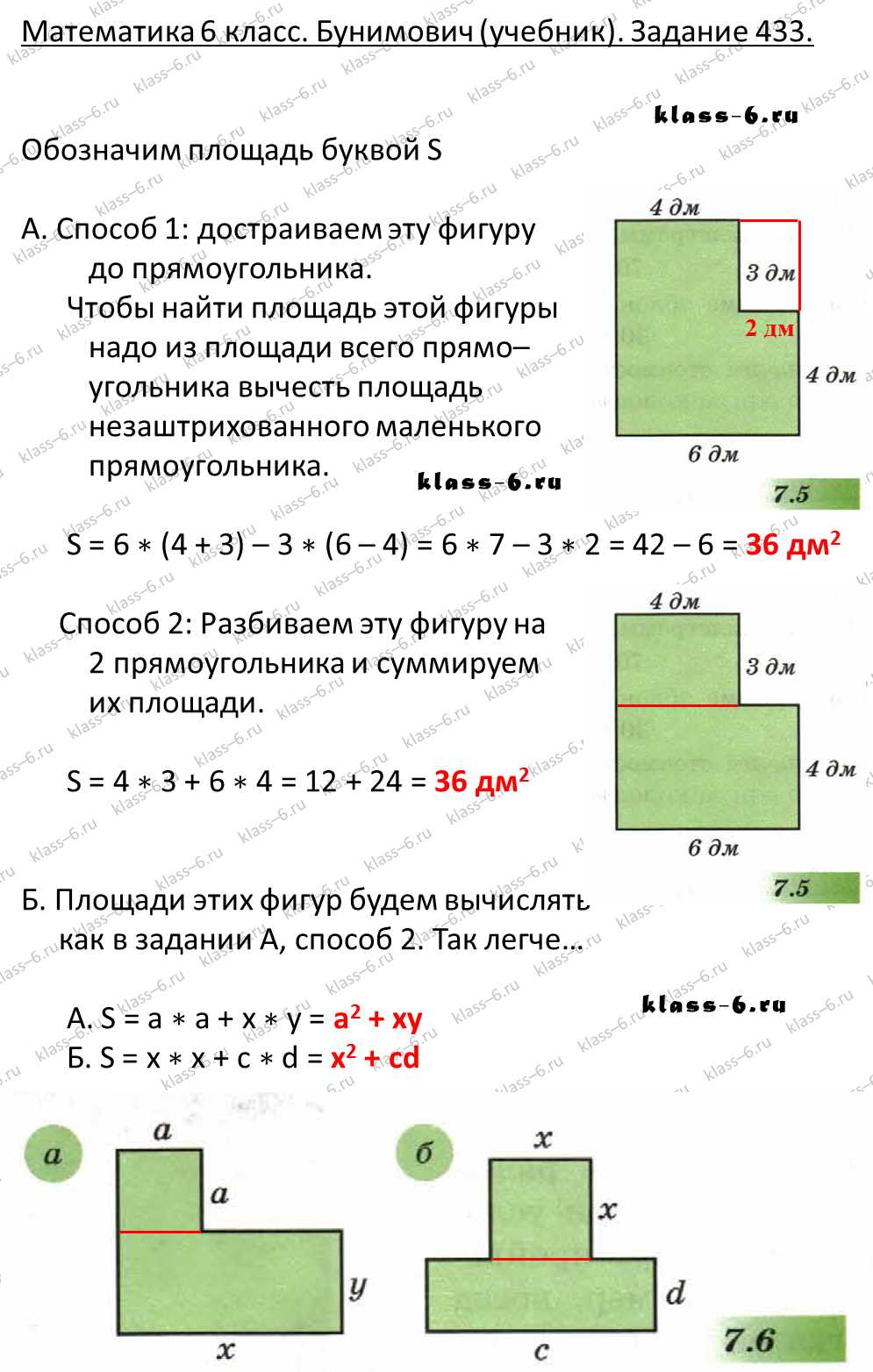
Основной шаг в процессе измерения площади звезды с помощью геометрических форм – это разбиение ее на более простые фигуры. В данном случае, прямоугольники будут основными формами, которые будут использоваться для измерения площади звезды.
Прямоугольник – это основная геометрическая форма, используемая для измерения площади звезды. Он имеет две стороны: длину и ширину, которые могут быть различными. Для измерения площади звезды с помощью прямоугольника, необходимо определить длину и ширину каждого прямоугольника, а затем использовать формулу для расчета его площади.
Одной из основных формул для расчета площади прямоугольника является формула: S = a * b, где S – площадь прямоугольника, a – длина прямоугольника, b – ширина прямоугольника. В данном случае каждый прямоугольник будет представлять собой часть звезды, и для каждого прямоугольника будут определены его длина и ширина.
Второе важное понятие при измерении площади звезды – это коэффициент. Коэффициент – это число, которое используется для умножения площади прямоугольника в случае, если его ширина не равна ширине звезды. Коэффициент позволяет учесть различия в ширине карте прямоугольников для получения правильного значения площади звезды.
Для получения точного значения площади звезды с помощью геометрических форм и прямоугольников, рекомендуется провести несколько измерений и применить коэффициент для каждого прямоугольника, чтобы полученная сумма площадей была максимально близка к реальной площади звезды.
Использование метода измерения площади звезды с помощью геометрических форм имеет множество приложений в разных областях. От учебного использования в классе до практических задач и научных исследований, этот метод предоставляет возможность получить конкретные численные значения площади звезды.
Использование формулы для расчета площади звезды
В одном из уроков-моделирования можно использовать палетки или клетчатую основу, чтобы наглядно продемонстрировать, как измеряется площадь звезды. С помощью простых элементарных действий ученикам предлагается переопределить площадь, измерив ширину звезды и раскрасив каждую клетку внутри. Такой метод измерения площади широко используется в классе.
Измерение площади с помощью диагоналей
Вместо измерения ширины звезды, можно использовать формулу для нахождения ее площади. Для этого нужно знать ее радиус и длину диагоналей. Формула для расчета площади звезды отличается от формулы для расчета площади прямоугольника. Математики изучают такие формулы и находят ответы на теоретические и практические вопросы нашей статьи.
Примеры вычисления площади с использованием формулы
Для лучшего понимания применения формулы в практике, приведем примеры вычисления площади звезды. Например, звезда имеет радиус 5 см и длину обеих диагоналей 10 см. Для рассчета ее площади, достаточно воспользоваться формулой и подставить значения: S = (0.5 * радиус * длина первой диагонали) + (0.5 * радиус * длина второй диагонали). Получившийся результат даст нам искомую площадь звезды.
Примеры вычисления площади звезды с использованием формулы
В этом разделе мы рассмотрим, как можно вычислить площадь звезды при помощи формулы. Такой способ позволяет получить более точные результаты в сравнении с использованием геометрических форм.
Для начала, давайте вспомним формулу для нахождения площади плоской фигуры: S = a * b, где S — площадь, a — длина, b — ширина. Однако, звезды не всегда имеют прямоугольную форму, поэтому нам нужно использовать формулы, специально разработанные для данного случая.
Существует несколько формул для вычисления площади звезды, в зависимости от ее формы. Одна из таких формул основана на использовании диаметра и пентаграммы внутри звезды. Пусть d — диаметр этой пятиугольной фигуры, тогда площадь звезды можно вычислить по формуле: S = (sqrt(5 * (5 + 2 * sqrt(5))) * (d^2)) / 4. Здесь sqrt — квадратный корень. Данная формула основана на свойствах выпуклого пятиугольника.
Если у вас нет диаметра пентаграммы, но есть длины сторон звезды, можно использовать другую формулу, основанную на длинах сторон и угла между ними. Для этого понадобится нахождение диагоналей и вычисление площади треугольников по формуле Герона. Это более сложный и численный метод, но он позволяет вычислить площадь звезды, даже если у вас нет диаметра или пентаграммы.
На уроке по геометрии, после изучения основных формул для нахождения площади звезды, пусть ученики решат несколько практических задач, чтобы закрепить полученные знания. Например, пусть каждый ученик нарисует звезду произвольной формы и вычислит ее площадь, используя одну из формул, которую они изучили.
Таким образом, использование разнообразных формул для вычисления площади звезды позволяет получить более точные и менее переопределенные решения. Оно также широко применяется в школьном курсе геометрии, чтобы научить учеников применять формулы и развивать навыки расчета площадей различных фигур. Это важное умение, которое может быть полезно не только на уроке, но и в реальной жизни при решении различных задач.
Применение практических задач для закрепления знаний
В этом разделе статьи мы рассмотрим, как можно применить полученные знания о площади звезды в школьном классе. Умение вычислить площадь фигуры может быть полезным не только в геометрии, но и во многих других областях.
Задачи с разнообразными геометрическими формами
Статья предлагает разнообразные практические задачи, которые помогут ученикам лучше усвоить методы вычисления площади. Задачи могут быть представлены в виде картинок или текстовых описаний. Пусть ученики решают задачи, требующие вычисления площади прямоугольника, окружности или даже необычной клетчатой формы.
Задачи с разбиением на части
Одна из интересных задач может быть связана с разбиением фигуры на несколько частей. Ученики должны уметь разбить фигуру на простые геометрические формы, для которых уже известна формула вычисления площади. Это поможет им понять, как суммировать площади разных частей, чтобы получить общую площадь фигуры.
Решая такие задачи, ученики не только закрепляют свои знания о формулах, но и развивают умение решать сложные геометрические задачи. Также это упражнение полезно для развития логического мышления, а также навыков работы с числовыми выражениями и вычислениями.
Знание площади прямоугольника и других геометрических фигур позволяет ученикам легко решать задачи из разных областей знаний. Вычисление площади может быть полезным не только в геометрии, но и в архитектуре, строительстве, картографии, а также при решении различных задач в ежедневной жизни.
Познакомившись с этой полезной информацией, учащиеся нашего школьного класса смогут лучше усвоить материал о площади звезды, а также применить полученные знания на практике. Задачи, представленные в статье, помогут им развить умение вычислять площадь различных геометрических фигур и использовать эту информацию в решениях реальных задач.
Раздел №11: Методика нахождения площади изображенных фигур

В данном разделе статьи мы рассмотрим второе, более сложное, методика определения площади звезды, представленной на геометрической карте. Для его применения требуется разбиение фигуры на более простые геометрические фигуры и использование специальных алгоритмических формул.
Для начала работы необходимо детально изучить изображенную звезду на геометрической карте и определить основные фигуры, из которых она состоит. Также необходимо учесть условия и требования, указанные в задании, так как некоторые задачи могут требовать использования переопределенных алгоритмических формул.
Для решения задач по нахождению площади звезды мы можем использовать разнообразные геометрические фигуры, такие как прямоугольники, треугольники, окружности и другие популярные формы. Необходимо выбрать нужные формулы для нахождения площади каждой отдельной фигуры и обобщить их решением в единую методику.
Для проведения работы рекомендуется использовать бумагу и карандаш для более точного измерения и разметки фигур. Можно создать таблицу, где перечислить все изображенные фигуры и расположить рядом с ними нужные формулы для нахождения их площади.
Пример работы методики:
| Фигура | Формула для расчета площади | Площадь |
|---|---|---|
| Прямоугольник | a * b | 12,5 кв. ед. |
| Треугольник | (a * h) / 2 | 7,2 кв. ед. |
| Окружность | π * r^2 | 2,3 кв. ед. |
| Общая площадь звезды | — | 22 кв. ед. |
Итак, в данном разделе мы рассмотрели методику нахождения площади изображенных фигур в звезде. Для успешного решения задач требуется разделение фигуры на простые геометрические формы, выбор необходимых формул и их последовательное применение. Помимо этого, для закрепления полученных знаний рекомендуется использовать практические задачи и общую информацию о площади фигур в данном журнале.
Вычисление площади фигур: разнообразие методов и задач
Измерение площади фигур
Одним из основных методов вычисления площади фигур является использование формул. Формулы для расчета площади могут отличаться в зависимости от вида фигуры, например, для прямоугольника используется формула: площадь = длина * ширина. Другой метод — использование геометрических форм, например, вычисление площади прямоугольника с помощью измерения диагоналей.
Разнообразие задач и примеры решений
Понимание разнообразия задач и способов их решения позволяет ученикам легче усваивать материал. В статье приведены примеры вычисления площади фигур с использованием различных методов и формул. Например, вычисление площади прямоугольника по заданным сторонам, или вычисление площади треугольника по заданным параметрам. Каждый пример сопровождается подробным объяснением шагов решения, что помогает ученикам лучше понять алгоритмы вычислений.
Кроме того, в статье содержится полезная информация о площади прямоугольника. Здесь вы найдете объяснение, почему вычисление площади прямоугольника требует знания диаметра и сторон, а также как связаны понятия площади и периметра этого прямоугольника. Познакомившись с этим материалом, вы узнаете, почему формула для вычисления площади прямоугольника основывается на квадратных клеточках и разнообразии форм фигур.
Задачи и закрепление знаний
Помимо теоретического материала и примеров решений, статья включает практические задачи, которые помогут вам закрепить полученные знания и применить их на практике. Задачи представлены в разнообразной форме, от простых до сложных, и требуют тщательного выполнения шагов решения. Решение похожих задач развивает логическое мышление и умение применять полученные знания.

0 Комментариев