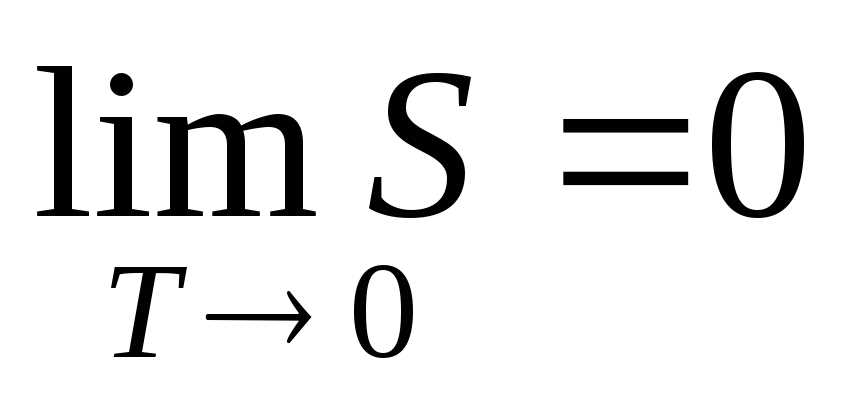
Закономерности и принципы термодинамики играют особую роль в изучении процессов, связанных с энергией и тепловыми явлениями. Третий закон термодинамики, также известный как теорема Нернста-Планка, представляет собой одно из основных положений этой науки. В этой статье рассматривается роль третьего закона термодинамики и его влияние на термодинамические процессы.
Основное содержание закона связано с концепцией энтропии и изменением ее значений при приближении системы к абсолютному нулю по температуре. Такое состояние невозможно достичь на практике, поскольку требует бесконечно большого количества времени и энергии. Однако третий закон термодинамики объясняет, каким образом энергетические процессы могут приближаться к этому идеальному состоянию.
Для понимания третьего закона термодинамики необходимо рассмотреть молекулярный уровень вещества и его свойства. Важным понятием в этом контексте является мольная энтропия, которая выражает вероятность различных микро-состояний системы. Эта вероятность связана с энергетическими состояниями молекул и их скоростью или активацией. Величина мольной энтропии изменяется в зависимости от температуры, концентраций веществ и других параметров.
Теорема Нернста-Планка позволяет выразить эту величину через экспериментальные данные и постулированные законы природы. Она основывается на идеальном веществе, которое не является реальным, но позволяет сделать расчеты и получить значимые результаты. Третий закон термодинамики в контексте теоремы Нернста-Планка выражается в виде уравнения, описывающего изменение энергии системы при приближении к абсолютному нулю.
Третий закон термодинамики и его влияние на понимание природы энтропии

Основной принцип третьего закона термодинамики заключается в том, что при абсолютном нуле температуры, все молекулы вещества будут находиться в своем основном состоянии, а их энергетические уровни будут наименьшими. В этом состоянии вещество достигает минимальной энтропии и порядка. Таким образом, третий закон устанавливает, что уровень энтропии является мерой упорядоченности системы и тесно связан с температурой.
Зависимость между энтропией и температурой, определенная третьим законом, имеет важное значение для понимания процессов течения энергии и энтропии в системах. При снижении температуры вещества, энтропия снижается, и происходит увеличение упорядоченности молекул. Это связано с тем, что при низких температурах, молекулы становятся менее движущимися и упорядоченными, что приводит к уменьшению случайности и хаоса.
Теорема Нернста-Планка играет особую роль в понимании третьего закона термодинамики, она устанавливает соотношение между энтропией и абсолютным нулем. Согласно этой теореме, при стремлении температуры к абсолютному нулю, энтропия стремится к нулю. Это означает, что абсолютный нуль является неким идеальным состоянием, где все молекулы находятся в своем основном состоянии с минимальной энергией и упорядоченностью.
Понимание третьего закона и его влияния на природу энтропии позволяет лучше раскрыть суть различных процессов термодинамики. Это важно для расчета энергетических характеристик и понимания тепловых потоков в различных системах. Знание третьего закона термодинамики позволяет оценить, как энтропия вещества меняется в зависимости от температуры и как происходят процессы течения энергии в системах.
Взаимосвязь энтропии и абсолютного нуля в идеальном газе
Тепловая теорема Нернста устанавливает, что при приближении температуры идеального газа к абсолютному нулю, энтропия системы стремится к нулю. Это означает, что при абсолютном нуле температуры идеальный газ достигает минимальной энтропии, его молекулы находятся в наиболее упорядоченном состоянии.
Важно отметить, что в данной теории Нернста-Планка концепция энтропии строится на основе изменения энергии молекул идеального газа при различных концентрациях. Вследствие этого, при приближении к абсолютному нулю, энергия молекул уменьшается, и, следовательно, их активация и скорость реакции достигают минимальных значений.
Итак, третий закон термодинамики называют третьим началом термодинамики и изучает изменение энтропических характеристик идеального газа по мере приближения к абсолютному нулю. Тепловая теорема Нернста играет значительную роль в понимании энергетических свойств газа и его поведения при различных температурных условиях.
Пример: энтропийные изменения в идеальном газе
- При температуре выше абсолютного нуля (температура > 0 К), энтропия газа растет, молекулы обладают большей энергией и свободы движения.
- При температуре равной абсолютному нулю (температура = 0 К), энтропия газа достигает минимального значения, молекулы находятся в статистическом покое.
Таким образом, тепловая теорема Нернста позволяет установить взаимосвязь между энтропией идеального газа и его поведением при приближении к абсолютному нулю. Изучение энтропии вещества при различных температурах помогает понять изменения его термодинамических свойств и реакционной способности.
Ключевая концепция третьего закона термодинамики: теорема Нернста-Планка
Третий закон термодинамики, также известный как теорема Нернста-Планка, играет важную роль в понимании природы энтропии и связи с абсолютным нулем температуры. Эта концепция третьего закона термодинамики исследует энергетические характеристики системы, включая расчет концентраций и температурных значений.
В термодинамическом равновесии, мольная энтропия системы при абсолютном нуле температуры равна нулю. Это выражение связывает энтропию с нулевой температурой и позволяет взять в расчет термодинамические процессы на различных температурных уровнях.
Теорема Нернста-Планка и поверхности концентраций

В основе третьего закона термодинамики лежит теорема Нернста-Планка, которая устанавливает, что уровень энергии системы при абсолютном нуле температуры может быть достигнут только в пределе. Это значит, что концентрация вещества неопределенной чистоты приближается к константному значению, которое определяет идеальную кристаллическую структуру.
Поверхности концентраций, также известные как адиабатические поверхности, представляют собой фазовые диаграммы, отражающие зависимость концентрации вещества от температуры. Эти поверхности имеют особую важность при изучении термодинамических процессов, так как они позволяют оценить изменения концентрации при различных температурных условиях.
Расчет энергетических характеристик системы
Ключевая роль теоремы Нернста-Планка в термодинамике заключается в возможности расчета энергетических характеристик системы. Применение первого закона термодинамики позволяет выразить энергию системы через её внутреннюю энергию и работу, совершаемую над системой или совершаемую ею.
Уравнение Нернста-Планка позволяет выявить взаимосвязь между энтропией и абсолютным нулем температуры. Оно позволяет оценить изменения энтропии системы при изменении ее температуры и концентрации вещества. В результате применения этого уравнения получается дополнительная информация о свойствах системы и ее энергетических характеристиках.
Расчет энергетических величин с использованием теоремы Нернста-Планка
В данном разделе мы рассмотрим роль теоремы Нернста-Планка в расчете энергетических характеристик процессов идеального газа. Эта теорема, основанная на термодинамических постулатах и уравнении изменения энтропии, позволяет определить скорость реакции и изменение энергетических параметров при различных температурах.
Основным выражением первого закона термодинамики для идеального газа является уравнение, связывающее изменение внутренней энергии газа с работой и теплом, участвующими в процессе. Используя теорему Нернста-Планка, мы можем определить, как энергия газа меняется в зависимости от температурного воздействия.
Уравнение изменения энтропии в процессе реакции газа, также известное как уравнение Больцмана, является ключевой концепцией третьего закона термодинамики. С помощью этого уравнения мы можем вычислить изменение энтропии, а следовательно и энергетические характеристики газа при различных температурах.
Теорема Нернста-Планка позволяет определить скорость реакции и ее зависимость от температуры в процессе. Исходя из этого, мы можем рассчитать энергетические характеристики газа при различных температурах, что нередко оказывается важным при проведении различных химических и физических экспериментов.
Роль теоремы Нернста-Планка в расчете энергетических величин в термодинамике
Рассматривая идеальный газ, который является основой термодинамических рассуждений, можно привести ключевую концепцию третьего закона термодинамики. Согласно данному постулату Нернста, при достижении абсолютного нуля температуры все тела становятся абсолютно неподвижными, и их энергия термодинамически равна нулю.
- Закон Нернста говорит о невозможности достижения температуры ниже абсолютного нуля. Это равновесное состояние газа находится на границе возможности и является основой для расчетов энергетических величин.
- Третье начало термодинамики утверждает, что при приближении к абсолютному нулю температуры, энтропия материала стремится к значению равному нулю.
- Идеальный газ в условиях нулевой температуры становится абсолютно неподвижным и достигает своего низшего возможного энергетического состояния.
Таким образом, теорема Нернста-Планка играет важную роль в термодинамике, обеспечивая понимание зависимости между энтропией и абсолютным нулем температуры. Она помогает в расчете энергетических характеристик системы и определении состояния газа при различных условиях, обеспечивая надежную основу для изучения процессов и течений в рамках термодинамического закона.
Основные выражения первого закона термодинамики для идеального газа
Определение идеального газа состоит в его представлении как газа, в котором молекулы взаимодействуют друг с другом и с окружающей средой только столкновениями, не обладая при этом никакими притяжениями или отталкиваниями друг от друга. Такое представление позволяет существенно упростить математическое описание газовых процессов и получить аналитические выражения для различных физических величин.
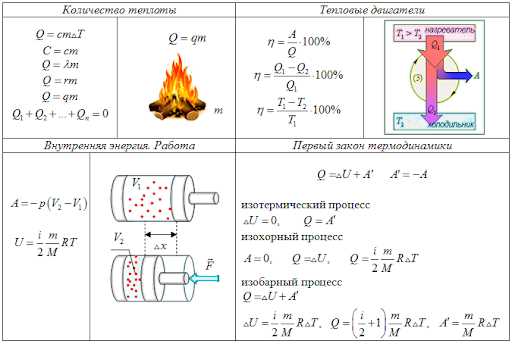
В выражениях первого закона термодинамики для идеального газа рассматриваются две основные характеристики системы: внутренняя энергия и работа, совершаемая газом на окружающую среду. Данное выражение позволяет рассчитать изменение внутренней энергии системы в зависимости от работы, совершенной газом.
Для идеального газа выражения первого закона термодинамики могут быть представлены в нескольких формах, включая молекулярные и молярные значения. Существует также связь теплоемкости идеального газа с изменением его внутренней энергии, которая является важной характеристикой газовых процессов. Эта зависимость может быть описана с использованием уравнений тепловой теоремы Нернста.
Таким образом, выражение первого закона термодинамики для идеального газа является ключевым в определении внутренней энергии и работы, а также связи между теплоемкостью и изменением внутренней энергии. Изучение данных выражений позволяет более глубоко понять и анализировать газовые процессы и их энергетические характеристики.
Реакции и катализ в термодинамике

Реакции газов могут происходить при определенных значениях энергии и температуры. Однако, для осуществления этих реакций и достижения желаемых результатов, проведения реакции требуется катализатор. Катализаторы могут влиять на скорость реакций, ускоряя или замедляя их ход. В термодинамике важна именно эффективность катализа для определения энергетических изменений в системе.
Если рассматривать процессы реакций в термодинамическом контексте, то можно сказать, что катализаторы играют ключевую роль в управлении направлением и скоростью реакций газовых смесей. Они обеспечивают оптимальные условия для протекания реакций, сохраняя энергию и приводя систему в состояние, где энергетические изменения максимальны.
Третий закон термодинамики позволяет определить энергетические характеристики процессов газовых реакций при наличии катализаторов и определить оптимальные условия для проведения этих реакций. Катализаторы играют важную роль в термодинамике, обеспечивая эффективное протекание реакций при минимальных потерях энергии. Таким образом, понимание и применение катализа в термодинамической системе является ключевым аспектом для оптимизации реакций газов и достижения желаемых энергетических результатов.
Термодинамика процессов идеального газа: энергетические характеристики и изменения температуры и давления
Один из ключевых аспектов исследования термодинамики заключается в изучении энергетических характеристик процессов идеального газа. В этом разделе мы рассмотрим важные понятия, связанные с изменением температуры и давления в таких процессах, а также принципы идеального газа, одной из основных концепций третьего начала термодинамики.
Одним из ключевых понятий, связанных с процессами идеального газа, является теплоемкость. Теплоемкость определяет количество теплоты, необходимое для изменения температуры системы при постоянном давлении. Это важная характеристика, учитывающая термодинамические свойства идеального газа в рамках третьего начала термодинамики.
Другим важным аспектом, который необходимо рассмотреть при изучении процессов идеального газа, является изменение давления. Давление влияет на поведение газовой системы и является одним из ключевых параметров для описания ее состояния. При изменении давления происходят энергетические переходы между различными состояниями системы, что имеет прямое отношение к первому закону термодинамики.
Осуществление процессов идеального газа требует учета не только температурных изменений и давления, но и энергетических характеристик системы. Следующим важным аспектом в изучении процессов идеального газа является применение первого закона термодинамики, который описывает сохранение энергии в системе идеального газа при проведении различных процессов.
Важно отметить, что применение идеального газа в исследовании термодинамики имеет широкий спектр приложений и позволяет рассмотреть различные энергетические характеристики процессов. Анализируя процессы идеального газа, мы можем более полно понять основные принципы термодинамики и их влияние на различные аспекты нашей жизни.

0 Комментариев